Beispiele für Verfahren zur Klassifikation von Daten
Im ersten Teil auf diesem Blog haben wir schon einiges über das statistische Verfahren der Clusteranalyse berichtet. Nun werden wir an den schon vorgestellten Beispiel-Daten zwei Algorithmen testen, welche beide das Ziel haben große Datenmengen in verhältnismäßiger Zeit zu klassifizieren. Dabei werden wir sehen, dass die Ergebnisse dabei sehr unterschiedlich ausfallen können.
Clusteranalyse: Der k-Means Algorithmus
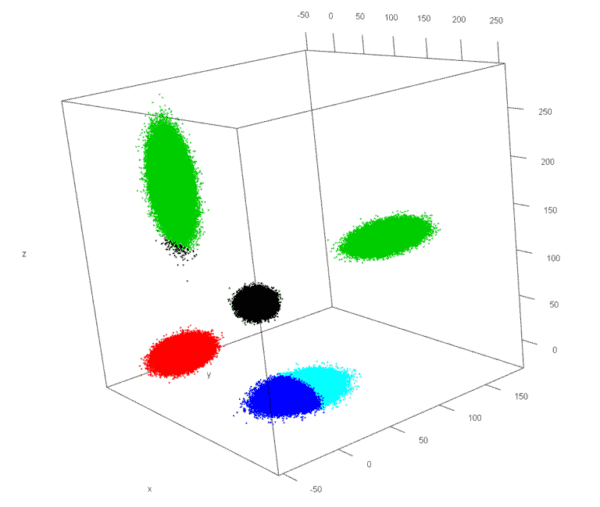
Abbildung 2: Plot k-Means Algorithmus
Dieser Algorithmus basiert darauf, dass zuvor eine feste Anzahl k von Klassen festgelegt werden muss und sich jede Klasse über ihren Schwerpunkt bzw. Mittelwert (engl. Mean) von den anderen unterscheidet. Deshalb sollte also vor der Analyse die Anzahl der vorliegenden Klassen bekannt sein. Im ersten Schritt werden zufällig k Objekte als Startwerte ausgewählt. Diese repräsentieren zunächst die k Klassen. Die restlichen Objekte werden derjenigen Klasse zugeordnet, zu dessen Startpunkt sie die größte Ähnlichkeit vorweisen. Nach erfolgreicher Zuteilung aller Objekte, werden pro Klasse die Schwerpunkte berechnet. Vergleichbar ist diese Berechnung mit der einfachen Mittelwertbildung über alle Objekte in einem Cluster. Mit den neuen Schwerpunkten als Startwerte beginnt der k-Means Algorithmus erneut. Das wird so lange wiederholt, bis kein Objekt mehr in einem Durchlauf einer anderen Klasse zugeordnet wird wie im Durchlauf zuvor. Daraufhin ist die finale Einteilung dann das Ergebnis der Clusteranalyse.
Leider ist dieses Verfahren sehr von den initialen Startwerten abhängig (siehe Abb. 2). Die Anwendung auf den Beispieldatensatz zeigt ein zwar mathematisch völlig korrektes, jedoch auch nicht optimales Ergebnis. Zwei der vorliegenden Cluster wurden beinahe richtig erkannt (rot und schwarz). Allerdings die grüne Klasse umfasst zwei der fünf Anhäufungen, weshalb die letzte Blase in die beiden blauen Cluster geteilt wurde. Hätte das Verfahren mit anderen Startwerten begonnen, hätten alle Cluster wie erwartet zugeordnet werden können oder aber es wäre ein weiteres falsch interpretierbares Ergebnis herausgekommen.
Verhindern lässt sich dieses Phänomen dadurch, den gesamten Algorithmus mehrmals hintereinander auszuführen und mit Hilfe einer Gütefunktion das „beste“ Ergebnis zu bestimmen. In den meisten Fällen wird dann die natürliche Struktur innerhalb der Datenmenge richtig erkannt. Jede weitere Ausführung des Algorithmus verlängert jedoch die Laufzeit erheblich.
Clusteranalyse: Der BIRCH Algorithmus
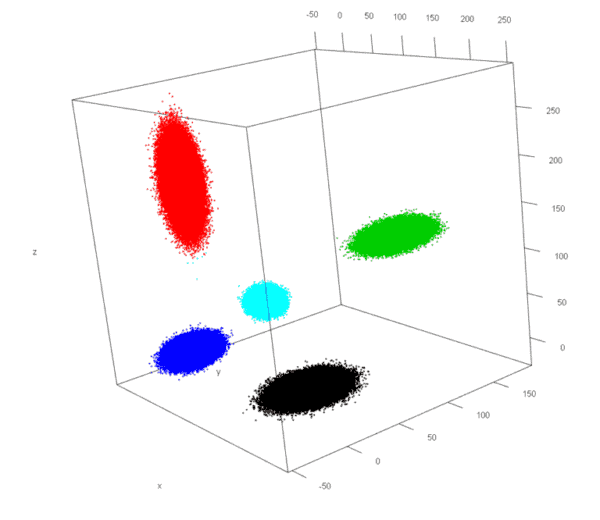
Abbildung 3: Plot BIRCH Algorithmus
Der BIRCH-Algorithmus besteht grundsätzlich aus zwei Schritten. Zunächst werden die Daten mit Hilfe einer Baumstruktur „vorklassifiziert“. Das ergibt in unserem Beispiel, dass die 1 Mio. Objekte schon zu etwa nur noch 2000 Gruppen von Klassen zusammengefasst werden. Aufgrund der Reduzierung des Umfangs kann dann eine klassische Clusteranalyse auf die Daten angewendet werden. Diese Verfahren beruhen darauf, dass am Anfang jedes Objekt eine eigene Klasse darstellt. In jedem Schritt werden dann die zwei Klassen zusammengefügt, welche die größte Ähnlichkeit zueinander aufweisen und das Ergebnis wird zwischengespeichert, solange bis die nur noch eine allumfassende Klasse vorhanden ist. Der Algorithmus wählt dann das Ergebnis aus, das die Ähnlichkeit innerhalb eines Clusters und Unterschiede zwischen den Clustern am besten beschreibt.
Im Gegensatz zum k-Means wird also auch die Anzahl an vorhandenen Klassen selbstständig erkannt und das Endergebnis entspricht in den meisten Fällen der tatsächlich vorliegenden Struktur (siehe Abb. 3). Die bessere Genauigkeit dieser clusteranalytischen Verfahren wird jedoch aus einer sehr viel höheren Komplexität gewonnen. Im Klartext heißt dies, um brauchbare Ergebnisse mit BIRCH zu erzielen, sind sehr viel mehr statistische Kenntnisse nötig, um die maximale Effizienz aus dem Verfahren herauszuholen.
Fazit
Die Clusteranalyse kann in vielen Fällen helfen sich einen Überblick über große Datenmenge zu verschaffen. Besonders im Big Data Bereich ist dies nötig, um so Ausreißer zu identifizieren oder die Daten zu segmentieren. Die beiden vorgestellten Verfahren bieten dabei zusammengefasst folgende Vor- und Nachteile:
k-Means
Vorteile:
- Einfach anzuwenden
- Von vielen Statistik Programmen standardmäßig implementiert
- Liefert in vielen Fällen ein brauchbares Ergebnis
Nachteile:
- Klassenanzahl muss vorher bekannt sein
- Ergebnis kann, abhängig von den Startwerten, eine andere Struktur als die natürliche Struktur wiedergeben
- Erhöhte Genauigkeit erfordert sehr viel mehr Laufzeit
BIRCH
Vorteile:
- In den meisten Fällen wird die natürliche Struktur erkannt
- Variable Einstellung, um auf unterschiedliche Datenbeschaffungen einzugehen
- Sehr schnelle Laufzeit, auch bei großen Datenmengen
- Klassenanzahl wird selbstständig erkannt
Nachteile:
- Verfahren nicht weit verbreitet in gängigen Statistikprogrammen
- Hohes Maß an statistischem Wissen nötig
- Durch die Vorklassifizierung geht Information verloren
Neben den beiden vorgestellten Algorithmen gibt es natürlich noch eine Vielzahl weiterer Methoden, die sich mit der gleichen Fragestellung befassen und die je nach Fall bessere und schlechtere Ergebnisse liefern können. Jedoch haben wir die Erfahrung gemacht, dass bereits diese beiden Verfahren ausreichen, um aus großen Datenmengen tiefgehende Erkenntnisse zu ziehen. Aus unserer Sicht ist die Clusteranalyse ein verhältnismäßig einfaches Verfahren, das statistisch verlässliche Insights liefert und damit ein fester Bestandteil im Repertoire eines Analysten sein sollte.



[…] zweiten Teil dieses Artikels werden wir die zwei Verfahren vorstellen, welche das Problem mit unterschiedlichen […]